84 - Largest Rectangle in Histogram
题目
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = 1
[2,1,5,6,2,3]

The largest rectangle is shown in the shaded area, which has area = 1
10
Example:
1
2
Input: [2,1,5,6,2,3]
Output: 10
分析
给一个直方图,用一系列非负数字表示,每个bar的宽度一样都为1,找到直方图中最大的矩形区域。
1) 暴力解法
就是以每个点为起点,向两边扩散,计算以当前高度为矩形的最大区域值,为此,需要:
- 左边看一下,看最多能向左延伸多长,找到大于等于当前柱形高度的最左边元素的下标;
- 右边看一下,看最多能向右延伸多长;找到大于等于当前柱形高度的最右边元素的下标。
对于每一个位置,都这样操作,得到一个矩形面积,然后取所有值中最大的那个,时间O(n^2),空间O(1)。

2)优化解法
时间换空间,暴力解法是每个柱子都两边扩散去找大于等于自己的柱子,有没有可能把柱子高度的信息先存储下来,直接用O(1)的方式来找呢?先思考一个问题:
对于i左边的两根柱子 j0以及 j1,如果索引 j0 在 j1右侧,并且 heights[j0] ≥ heights[j1],那么对于任意的在j0和j1之后出现的柱子 i (j1 < i),j0一定不会是位于 i 左侧的最近的小于其高度的柱子。
以题目中的[2,1,5,6,2,3]为例:
1、一开始看到的柱形高度为 1
2
1
2

2、然后看到到高度为 1 的柱形,这个时候以这个柱形为高度的矩形的最大面积还是不知道的。但是它之前的以 2 为高度的最大面积的矩形是可以确定的,这是因为这个 1 比 2 小 ,因为这个 1 卡在了这里 2 不能再向右边扩展了,如下图。

计算一下以 2 为高度的最大矩形的面积是 2。如果已经确定了一个柱形的高度,接下来的计算这个矩形可以不管了,将它以虚框表示,如下图。

3、遍历到高度为 5 的柱形,同样的以当前看到柱形为高度的矩形的最大面积也是不知道的,因为还要看右边高度的情况。那么它的左右有没有可以确定的柱形呢?没有,这是因为 5 比 1 大,我们看后面马上就出现了 6,不管是 1 这个柱形还是 5 这个柱形,都还可以向右边扩展。

4、接下来,遍历到高度为 1
6
1
1
1
5
1
6

5、再接下来,遍历到高度为 1
2

发现了一件很神奇的事情,高度为 6 的柱形对应的最大矩形的面积的宽度可以确定下来,它就是夹在高度为 5 的柱形和高度为 2 的柱形之间的距离,它的高度是 6,宽度是 1。

将可以确定的柱形设置为虚线

接下来柱形 1
5
1
1
1
2

标成虚线

我们发现了,只要是遇到了当前柱形的高度比它上一个柱形的高度严格小的时候,一定可以确定它之前的某些柱形的最大宽度,并且确定的柱形宽度的顺序是从右边向左边。 这个现象告诉我们,在遍历的时候需要记录的信息就是遍历到的柱形的下标,它一左一右的两个柱形的下标的差就是这个面积最大的矩形对应的最大宽度。
这个时候,还需要考虑的一个细节是,在确定一个柱形的面积的时候,除了右边要比当前严格小,其实还蕴含了一个条件,那就是左边也要比当前高度严格小。
那如果是左边的高度和自己相等怎么办呢?之前是只要比当前严格小,才可以确定一些柱形的最大宽度。只要是大于或者等于之前看到的那一个柱形的高度的时候,其实都不能确定。因此确定当前柱形对应的宽度的左边界的时候,往回头看的时候,一定要找到第一个严格小于我们要确定的那个柱形的高度的下标。这个时候中间那些相等的柱形其实就可以当做不存在一样。因为它对应的最大矩形和它对应的最大矩形其实是一样的。
我们在遍历的时候,需要记录的是下标,如果当前的高度比它之前的高度严格小于的时候,就可以直接确定之前的那个高的柱形的最大矩形的面积,而为了确定这个最大矩形的左边界,还要找到第一个严格小于它的高度的矩形,向左回退的时候,其实就可以当中间这些柱形不存在。
这是因为我们就是想确定 6 的宽度,6 的宽度确定完了,其实我们就不需要它了,这个 5 的高度和这个 5 的高度确定完了,也不需要它了。在缓存数据的时候,是从左向右缓存的,我们计算出一个矩形的面积的顺序则是从右向左的,并且计算完成以后就不再需要了,符合后进先出的特点。因此,我们需要的这个作为缓存的数据结构就是栈。当确定了一个柱形的高度的时候,就将它从栈顶移出,所有的柱形在栈中进栈一次,出栈一次,一开始栈为空,最后也一定要让栈为空,表示这个高度数组里所有的元素都考虑完了。
6、最后遍历到最后一个柱形,即高度为 3 的柱形。

(一次遍历完成以后。接下来考虑栈里的元素全部出栈。)
接下来就要依次考虑还在栈里的柱形的高度。和刚才的方法一样,只不过这个时候右边没有比它高度还小的柱形了,这个时候计算宽度应该假设最右边还有一个下标为 len (这里index等于 6) 的高度为 0 (或者 0.5,只要比 1 小)的柱形,作为哨兵柱子。


7、下标为 5 ,即高度为 3 的柱形,左边的下标是 4 ,右边的下标是 6 ,因此宽度是 6 - 4 - 1 = 1(两边都不算,只算中间的距离,所以减 1);算完以后,将它标为虚线。

8、下标为 4 ,高度为 2 的柱形,左边的下标是 1 ,右边的下标是 6 ,因此宽度是 6 - 1 - 1 = 4;算完以后,将它标为虚线。

9、最后看下标为 1,高度为 1 的矩形,它的左边和右边其实都没有元素了,它就是整个柱形数组里高度最低的柱形,没有谁能挡住它,所以计算它的宽度,就是整个柱形数组的长度。


到此为止,所有的柱形高度对应的最大矩形的面积就都计算出来了。

Time:O(n);Space:新建一个Stack,O(n);
为什么这个方法是正确的呢?参考这里。

例如我们遇到最后遇到一个递减的bar(红色)。高度位于红线上方的(也就是算法中栈里面大于最右bar的)元素,他们是不可能和最右边的较小高度bar围成一个比大于在弹栈过程中的矩形面积了(黄色面积),因为红色的bar对他们来说是一个短板,和红色bar能围成的最大面积也就是红色的高度乘以这些“上流社会”所跨越的索引范围。但是“上流社会”的高度个个都比红色bar大,他们完全只计算彼此之间围成的面积就远远大于和红色bar围成的任意面积了。所以红色bar是不可能参与“上流社会”的bar的围城的(好悲哀)。
但是屌丝也不用泄气哦。因为虽然长度不占优势,但是团结的力量是无穷的。它还可以参与“比较远的”比它还要屌丝的bar的围城。他们的面积是有可能超过上流社会的面积的,因为距离啊!所以弹栈到比红色bar小就停止了。
另外一个细节需要注意的是,弹栈过程中面积的计算。
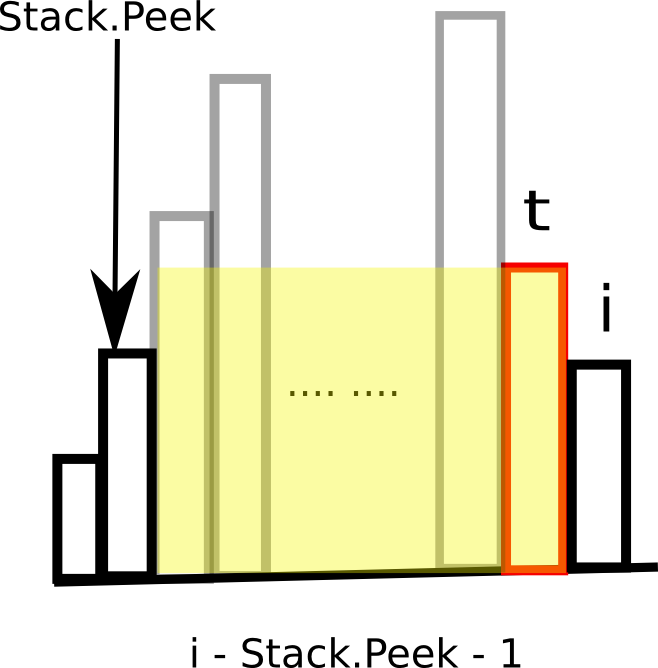
h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1)
h[t]是刚刚弹出的栈顶端元素。此时的面积计算是h[t]和前面的“上流社会”能围成的最大面积。这时候要注意,栈内索引指向的元素都是比h[t]小的,如果h[t]是目前最小的,那么栈内就是空!而在目前栈顶元素和h[t]之间(不包括h[t]和栈顶元素),都是大于他们两者的。如下图所示:
那h[t]无疑就是Stack.Peek和t之间那些上流社会的短板啦,而它们的跨越就是i - Stack.Peek - 1。
所以说,这个弹栈的过程也是维持程序不变量的方法啊:栈内元素一定是要比当前i指向的元素小的。

代码
暴力解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) {
return 0;
}
int len = heights.length;
int result = 0;
for (int i = 0; i < len; i++) {
int curHeight = heights[i];
// 找左边最后 1 个大于等于 heights[i] 的索引
int left = i - 1;
while (left >= 0 && heights[left] >= curHeight) {
left--;
}
// 找右边最后 1 个大于等于 heights[i] 的索引
int right = i + 1;
while (right < len && heights[right] >= curHeight) {
right++;
}
result = Math.max(result, (right - left - 1) * curHeight);
}
return result;
}
}
Stack + 哨兵解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) {
return 0;
}
int len = heights.length;
// 栈中存储柱子的index
Stack<Integer> stack = new Stack<>();
int result = 0;
for (int i = 0; i <= len; i++) { // 末尾会多一个哨兵节点
int height = (i == len) ? 0 : heights[i]; //判断一下哨兵节点
if (stack.isEmpty() || height >= heights[stack.peek()]) { // 单调递增,入栈
stack.push(i);
} else { // 当前柱子比前面的柱子矮了
int preIndex = stack.pop();
int currArea = 0;
if (stack.isEmpty()) { // pop到哨兵节点位置了,计算最矮的柱子乘以所有柱子数目的面积
currArea = heights[preIndex] * i;
} else { // 正常计算
currArea = heights[preIndex] * (i - 1 - stack.peek());
}
result = Math.max(result, currArea);
i--; // 继续退回前面高的柱子,看要不要pop然后计算面积
}
}
return result;
}
}