GuilinDev
Lc0087
05 August 2008
87. Scramble String
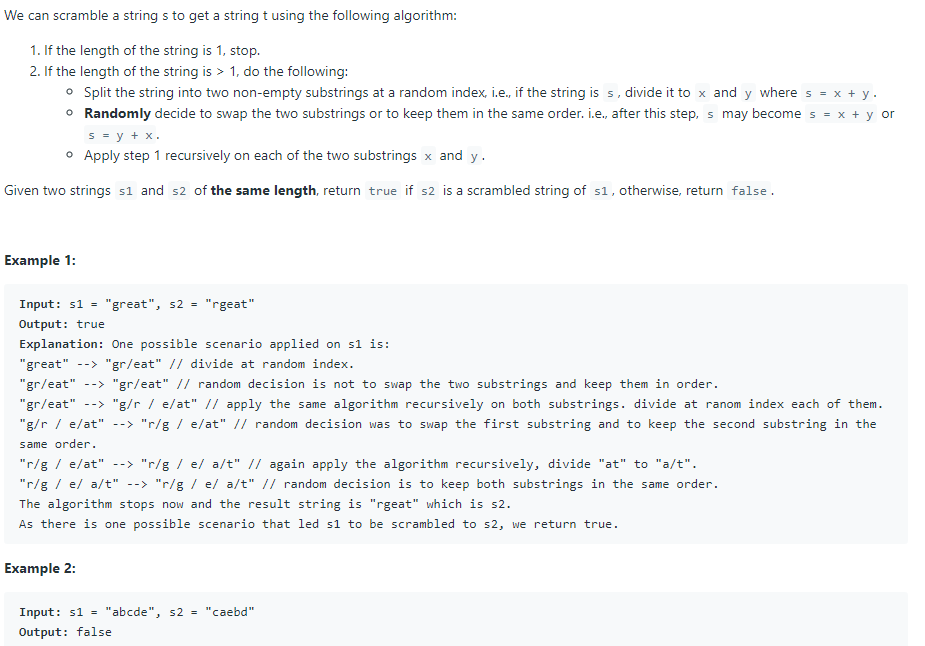
按照规则扰乱字符串，判断是否可以从s扰乱到t
top down
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public boolean isScramble(String s1, String s2) {
// 长度不等，必定不能变换
if (s1.length() != s2.length()) {
return false;
}
// 长度相等，先特判下
if (s1.equals(s2)) {
return true;
}
// 看一下字符个数是否一致，不同直接return false
int n = s1.length();
HashMap<Character, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
char c1 = s1.charAt(i);
char c2 = s2.charAt(i);
map.put(c1, map.getOrDefault(c1, 0) + 1);
map.put(c2, map.getOrDefault(c2, 0) - 1);
}
for (Character key : map.keySet()) {
if (map.get(key) != 0) {
return false;
}
}
// 相同的话，开始判断判断，满足一个就能 return true
for (int i = 1; i < n; i++) {
boolean flag =
// S1 -> T1，S2 -> T2
(isScramble(s1.substring(0, i), s2.substring(0, i)) && isScramble(s1.substring(i), s2.substring(i))) ||
// S1 -> T2，S2 -> T1
(isScramble(s1.substring(0, i), s2.substring(n - i)) && isScramble(s1.substring(i), s2.substring(0, s2.length() - i)));
if (flag) {
return true;
}
}
return false;
}
}
bottom up
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
public boolean isScramble(String s1, String s2) {
char[] chs1 = s1.toCharArray();
char[] chs2 = s2.toCharArray();
int n = s1.length();
int m = s2.length();
if (n != m) {
return false;
}
boolean[][][] dp = new boolean[n][n][n + 1];
// 初始化单个字符的情况
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j][1] = chs1[i] == chs2[j];
}
}
// 枚举区间长度 2～n
for (int len = 2; len <= n; len++) {
// 枚举 S 中的起点位置
for (int i = 0; i <= n - len; i++) {
// 枚举 T 中的起点位置
for (int j = 0; j <= n - len; j++) {
// 枚举划分位置
for (int k = 1; k <= len - 1; k++) {
// 第一种情况：S1 -> T1, S2 -> T2
if (dp[i][j][k] && dp[i + k][j + k][len - k]) {
dp[i][j][len] = true;
break;
}
// 第二种情况：S1 -> T2, S2 -> T1
// S1 起点 i，T2 起点 j + 前面那段长度 len-k ，S2 起点 i + 前面长度k
if (dp[i][j + len - k][k] && dp[i + k][j][len - k]) {
dp[i][j][len] = true;
break;
}
}
}
}
}
return dp[0][0][n];
}
}