GuilinDev

Lc0133

05 August 2008

133 Clone Graph

题目

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (‘int’) and a list (‘List[Node]’) of its neighbors.

1
2
3
4

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with ‘val = 1’, the second node with ‘val = 2’, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with ‘val = 1’. You must return the copy of the given node as a reference to the cloned graph.

Example 1: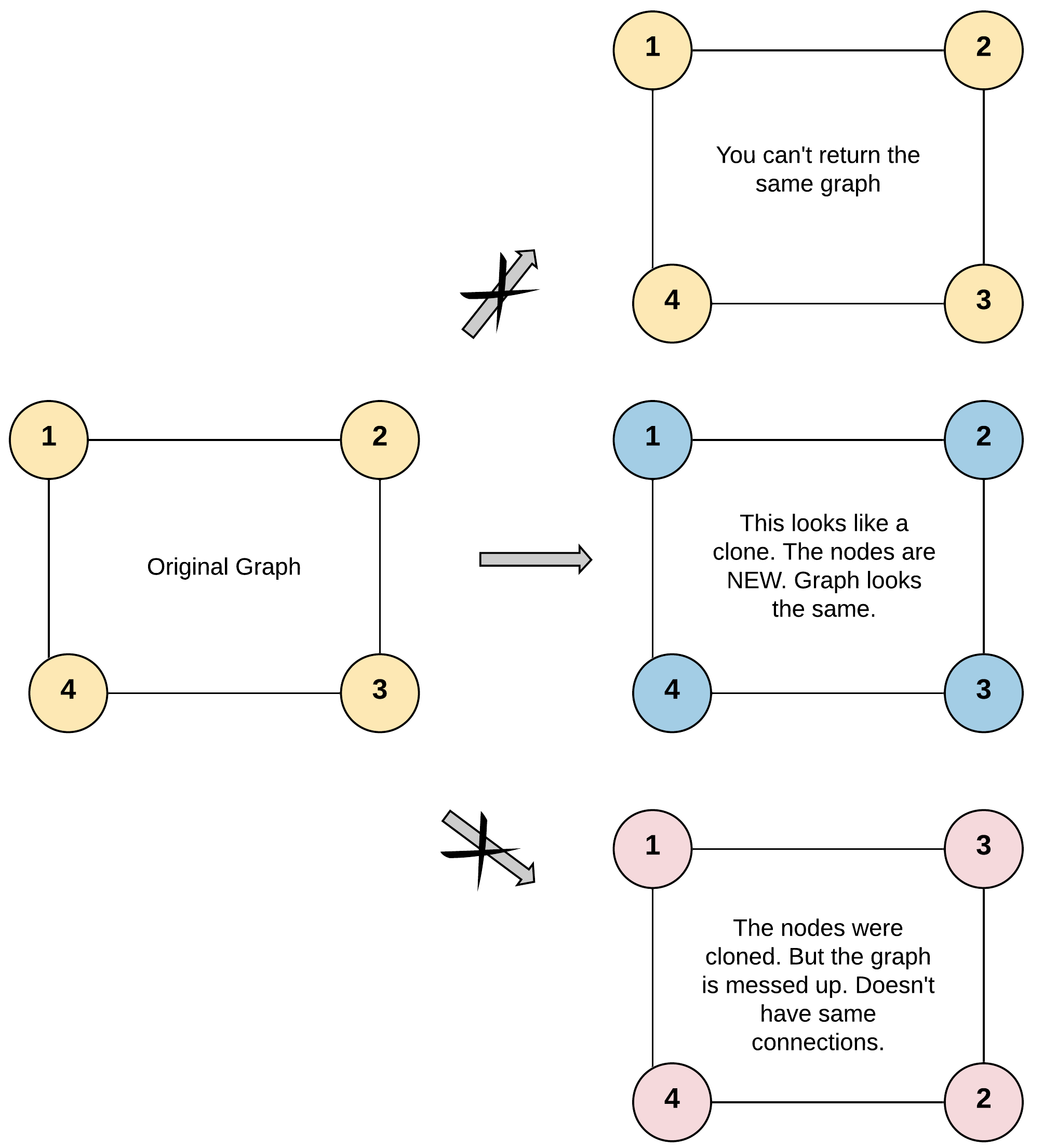

1
2
3
4
5
6
7

Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

1
2
3

Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

1
2
3

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

1
2

Input: adjList = [[2],[1]]
Output: [[2],[1]]

Constraints:

  • ‘1 <= Node.val <= 100’
  • ‘Node.val’ is unique for each node.
  • Number of Nodes will not exceed 100.
  • There is no repeated edges and no self-loops in the graph.
  • The Graph is connected and all nodes can be visited starting from the given node.

分析

思路很简单，就是图的DFS和BFS，两个都要重点掌握。

代码

DFS

  1. 从给定节点开始遍历图
  2. 使用一个 HashMap 存储所有已被访问和复制的节点。HashMap 中的 key 是原始图中的节点，value 是克隆图中的对应节点。如果某个节点已经被访问过，则返回其克隆图中的对应节点。
  3. 如果当前访问的节点不在 HashMap 中，则创建它的克隆节点存储在 HashMap 中。注意：在进入递归之前，必须先创建克隆节点并保存在 HashMap 中，否则递归会再次遇到同样节点，陷入死循环。
  4. 递归调用每个节点的邻接点。每个节点递归调用的次数等于邻接点的数量，每一次调用返回其对应邻接点的克隆节点，最终返回这些克隆邻接点的列表，将其放入对应克隆节点的邻接表中。这样就可以克隆给定的节点和其邻接点。

时间复杂度：O(N)，每个节点只处理一次。

空间复杂度：O(N)，存储克隆节点和原节点的 HashMap 需要 O(N) 的空间，递归调用栈需要 O(H) 的空间，其中 H 是图的深度。总体空间复杂度为 O(N)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    public Node cloneGraph(Node node) {
        HashMap<Node, Node> visited = new HashMap<>();
        return dfs(node, visited);
    }
    private Node dfs(Node node, HashMap<Node, Node> visited) {
        if (node == null) {
            return null;
        }
        if (visited.containsKey(node)) {
            return visited.get(node);
        }
        Node clone = new Node(node.val, new ArrayList<>()); //复制的节点和其neighbors
        visited.put(node, clone); // 需要在下面dfs之前添加已被访问和复制
        for (Node n : node.neighbors) {// 递归添加neighbors到复制节点上
            clone.neighbors.add(dfs(n, visited));
        }
        
        return clone;
    }
}

BFS，考虑到调用栈的深度，使用 BFS 进行图的遍历比 DFS 更好。BFS也需要借助 HashMap 避免陷入死循环。

  1. 使用 HashMap 存储所有访问过的节点和克隆节点。HashMap 的 key 存储原始图的节点，value 存储克隆图中的对应节点。visited 用于防止陷入死循环，和获得克隆图的节点。
  2. 将第一个节点添加到队列。克隆第一个节点添加到名为 ‘visited’ 的 HashMap 中。
  3. BFS 遍历
    1. 从队列首部取出一个节点。
    2. 遍历该节点的所有邻接点。
    3. 如果某个邻接点已被访问，则该邻接点一定在 ‘visited’ 中，那么从 ‘visited’ 获得该邻接点。
    4. 否则，创建一个新的节点存储在 ‘visited’ 中。
    5. 将克隆的邻接点添加到克隆图对应节点的邻接表中。

时间复杂度：O(N)，每个节点只处理一次。

空间复杂度：O(N)。visited 使用 O(N) 的空间。BFS 中的队列使用 O(W) 的空间，其中 W 是图的宽度（比DFS中的深度要小）。总体空间复杂度为 O(N)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
    public Node cloneGraph(Node node) {
        if (node == null) {
            return null;
        }
        HashMap<Node, Node> visited = new HashMap<>(); // 保存访问信息和复制信息
        
        Queue<Node> queue = new LinkedList<>();
        queue.add(node);
        
        visited.put(node, new Node(node.val, new ArrayList<>())); // 先把第一个node标记访问和复制
        
        while (!queue.isEmpty()) {
            Node curNode = queue.poll();
            
            // 遍历当前节点的所有neighbors
            for (Node neighbor : curNode.neighbors) {
                if (!visited.containsKey(neighbor)) {
                    // 把neighbor节点加入到visited中
                    visited.put(neighbor, new Node(neighbor.val, new ArrayList<>()));
                    // 把新节点加入到队列中
                    queue.offer(neighbor);
                }
                
                // 添加当前节点的复制节点的neighbors信息
                visited.get(curNode).neighbors.add(visited.get(neighbor));
            }
        }
        return visited.get(node);
    }
}
This site is open source. Improve this page.