GuilinDev
Lc0221
05 August 2008
221 Maximal Square
01矩阵只含1的最大正方形 - DP
dp[i][j] - 在i，j位置为止时最大的正方形的边长长度
如果该位置的值是 0，则 dp(i,j)=0，因为当前位置不可能在由 1 组成的正方形中；
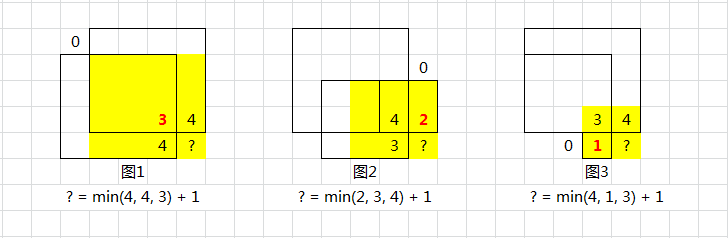
如果该位置的值是 1，则 dp(i,j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值(类似木桶短板理论，如图)加 1，状态转移方程如下：
dp(i, j)= min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1))+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public int maximalSquare(char[][] matrix) {
int maxSide = 0;
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return maxSide;
}
int rows = matrix.length, columns = matrix[0].length;
int[][] dp = new int[rows][columns];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1; //别忘记 + 1
}
maxSide = Math.max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
}
联系下，初始化放外面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public int maximalSquare(char[][] matrix) {
int maxLen = 0;
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return maxLen * maxLen;
}
int m = matrix.length, n = matrix[0].length;
int[][] dp = new int[m][n];
// 初始化放外面, 每次赋值maxLen感觉不好
for (int i = 0; i < m; i++) {
if (matrix[i][0] == '1') {
dp[i][0] = 1;
maxLen = Math.max(maxLen, dp[i][0]);
}
}
for (int j = 0; j < n; j++) {
if (matrix[0][j] == '1') {
dp[0][j] = 1;
maxLen = Math.max(maxLen, dp[0][j]);
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == '1') {
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
maxLen = Math.max(maxLen, dp[i][j]);
}
}
return maxLen * maxLen;
}
}