GuilinDev
Lc0223
05 August 2008
223 Rectangle Area
原题概述
Find the total area covered by two rectilinear rectangles in a 2D plane.
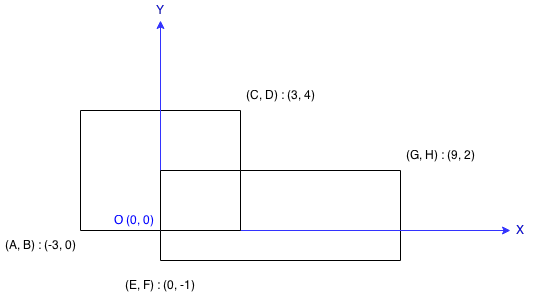
Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.
Example:
1
2
Input: A = -3, B = 0, C = 3, D = 4, E = 0, F = -1, G = 9, H = 2
Output: 45
Note:
Assume that the total area is never beyond the maximum possible value of int.
题意和分析
这道题考察我们能否全面的考虑到所有可能。如果两个矩形没有重叠部分，则直接计算两个矩形面积之和就行了。如果两个矩形有重叠部分，则要将重叠部分减去。如何判断两个矩形没有重叠部分呢，如果一个矩形右上角的横坐标比另一个矩形左下角的横坐标要小，或者一个矩形右上角的纵坐标比另一个矩形左下角的纵坐标要小，则两个矩形是不重叠的。因为两个矩形的坐标都可能比对方小，所以我们一共有四种可能情况是不重叠的。如果重叠的话，计算重叠部分面积就是四个横坐标中中间那两个和四个纵坐标中间那两个。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
int area1 = Math.abs(A - C) * Math.abs(B - D);
int area2 = Math.abs(E - G) * Math.abs(F - H);
//分别是横坐标相差和纵坐标，求出横纵坐标的相差，乘以得出重叠区
int common = overlap(A, C, E, G) * overlap(B, D, F, H);
return area1 + area2 - common; //两个矩形的面积相加，然后减去一个相交矩形的面积
}
private int overlap(int lowerLeft1, int upperRight1, int lowerLeft2, int upperRight2) {
if (lowerLeft1 >= upperRight2 || lowerLeft2 >= upperRight1) {//两个矩形不相交
return 0;
}
//两个lowerleft中的较大者在上面，两个upperRight中的较小者在下面，二者中间是重叠区域的长和宽
return Math.abs(Math.max(lowerLeft1, lowerLeft2) - Math.min(upperRight1, upperRight2));
}
}