GuilinDev

Lc0261

05 August 2008

261 Graph Valid Tree Medium $

You have a graph of 

1

n
nodes labeled from 
1

0
to 
1

n - 1
. You are given an integer n and a list of 
1

edges
where 
1

edges[i] = [ai, bi]
indicates that there is an undirected edge between nodes 
1

ai
and 
1

bi
in the graph.

Return 

1

true
if the edges of the given graph make up a valid tree, and 
1

false
otherwise.

Example 1: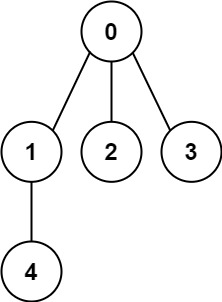

1
2

Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2: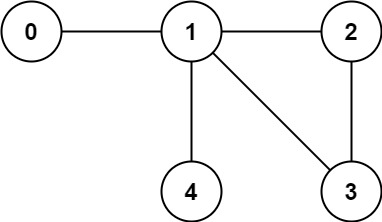

1
2

Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

Constraints:

  • 1

    1 <= 2000 <= n

  • 1

    0 <= edges.length <= 5000

  • 1

    edges[i].length == 2

  • 1

    0 <= ai, bi < n

  • 1

    ai != bi
  • There are no self-loops or repeated edges.

图的DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
    public boolean validTree(int n, int[][] edges) {
        // initialize adjacency list
        List<List<Integer>> adjList = new ArrayList<List<Integer>>(n);
        
        // initialize vertices
        for (int i = 0; i < n; i++)
            adjList.add(i, new ArrayList<Integer>());
        
        // add edges    
        for (int i = 0; i < edges.length; i++) {
            int u = edges[i][0], v = edges[i][1];
            adjList.get(u).add(v);
            adjList.get(v).add(u);
        }
        
        boolean[] visited = new boolean[n];
        
        // make sure there's no cycle
        if (hasCycle(adjList, 0, visited, -1))
            return false;
        
        // make sure all vertices are connected
        for (int i = 0; i < n; i++) {
            if (!visited[i]) 
                return false;
        }
        
        return true;
    }
    
    // check if an undirected graph has cycle started from vertex u
    boolean hasCycle(List<List<Integer>> adjList, int u, boolean[] visited, int parent) {
        visited[u] = true;
        
        for (int i = 0; i < adjList.get(u).size(); i++) {
            int v = adjList.get(u).get(i);
            
            if ((visited[v] && parent != v) || (!visited[v] && hasCycle(adjList, v, visited, u)))
                return true;
        }
        
        return false;
    }
}

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
    public boolean validTree(int n, int[][] edges) {
        int[] visited = new int[n];
        List<List<Integer>> adjList = new ArrayList<>();
        for (int i=0; i<n; ++i) { adjList.add(new ArrayList<Integer>()); }
        for (int[] edge: edges) {
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }
        if (hasCycle(-1, 0, visited, adjList)) { return false; }  // has cycle
        for (int v: visited) { if (v == 0) { return false; } }  // not 1 single connected component
        return true;
    }
    
    private boolean hasCycle(int pred, int vertex, int[] visited, List<List<Integer>> adjList) {
        visited[vertex] = 1;  // current vertex is being visited
        for (Integer succ: adjList.get(vertex)) {  // successors of current vertex
            if (succ != pred) {  // exclude current vertex's predecessor
                if (visited[succ] == 1) { return true; }  // back edge/loop detected!
                else if (visited[succ] == 0) {
                    if (hasCycle(vertex, succ, visited, adjList)) { return true; }
                }
            }
        }
        visited[vertex] = 2;
        return false;
    }
}

Union-Find with path compression and merge by rank

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
    
    class UnionFind {
        
        int[] parent;
        int[] rank;
        int count;
        
        UnionFind(int n) {
            parent = new int[n];
            rank = new int[n];
            count = n;  // number of components
            for (int i=0; i<n; ++i) { parent[i] = i; }  // initially, each node's parent is itself.
        }
        
        int find(int x) {
            if (x != parent[x]) {
                parent[x] = find(parent[x]);  // find root with path compression
            }
            return parent[x];
        }
        
        boolean union(int x, int y) {
            int X = find(x), Y = find(y);
            if (X == Y) { return false; }
            if (rank[X] > rank[Y]) { parent[Y] = X; }  // tree Y is lower
            else if (rank[X] < rank[Y]) { parent[X] = Y; }  // tree X is lower
            else {  // same height
                parent[Y] = X;
                ++rank[X];
            }
            --count;
            return true;
        }
    }
    
    public boolean validTree(int n, int[][] edges) {
        UnionFind uf = new UnionFind(n);
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            if (!uf.union(x, y)) { return false; }  // loop detected
        }
        return uf.count == 1;
    }
}
This site is open source. Improve this page.