GuilinDev

Lc0285

05 August 2008

285 Inorder Successor in BST

题目

Given a binary search tree and a node in it, find the in-order successor of that node in the BST.

The successor of a node 

1

p
is the node with the smallest key greater than 
1

p.val
.

Example 1: 

1
2
3

Input: root = [2,1,3], p = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both p and the return value is of TreeNode type.

Example 2: 

1
2
3

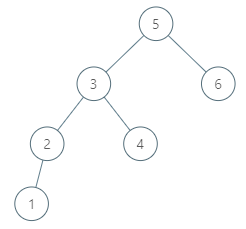
Input: root = [5,3,6,2,4,null,null,1], p = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Note:

  1. If the given node has no in-order successor in the tree, return 
    1

    null
    .
  2. It’s guaranteed that the values of the tree are unique.

分析

中序遍历结果是一个递增的数组，顺序后继是中序遍历中当前节点 之后 最小的节点。

方法1：递归执行中序遍历，获取一个list，在结果list中得到p的下一个。时间O(N)，空间O(N)

方法2： 递归执行中序遍历，在递归过程中获取x的下一个。如果当前值是<=x的，那么根据BST的特性只需要在右子树中找。如果当前值>x，则当前值有可能，它的左子树也有可能有更小的但是也>x的，对左子树递归后，选择更接近的（更小的)。时间O(logN)，空间O(logN)调用栈的深度。

方法3：方法2的循环实现，如果当前值是<=x的，那么根据BST的特性只需要在右子树中找：cur=cur.right。 如果当前值>x，则当前值有可能，它的左子树也有可能有更小的但是也>x的。则每次走入这个分支时，当前点是一个候选点，记录该节点的值和历史最小节点的值。 时间O(logN)，空间O(1）

代码

方法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    List<TreeNode> list;
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        list = new ArrayList<>();
        inOrder(root);
        
        TreeNode result = null;
        for (int i = 0; i < list.size(); i++) {
            if (list.get(i).val == p.val) {
                if (i != list.size() - 1) {
                    result = list.get(i + 1);
                }
            }
        }
        return result;
    }
    private void inOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        inOrder(node.left);
        list.add(node);
        inOrder(node.right);
    }
}

方法2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        return inOrder(root, p);
    }
    private TreeNode inOrder(TreeNode node, TreeNode p) {
        if (p == null || node == null) {
            return null;
        }
        if (node.val <= p.val) {//当前和左边都不可能大于p，继续递归右子树
            return inOrder(node.right, p);
        }
        //node > p
        TreeNode result = inOrder(node.left, p);
        if (result != null && result.val < node.val) {
            return result;
        } else {
            return node;
        }
    }
}

方法3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        if (p == null || root == null) {
            return null;
        }
        TreeNode curr = root;
        TreeNode result = null;
        while (curr != null) {
            if (curr.val <= p.val) {
                curr = curr.right;
            } else {
                if (result == null || result.val > curr.val) {
                    result = curr;
                }
                curr = curr.left;
            }
        }
        return result;
    }

}
This site is open source. Improve this page.