GuilinDev

Lc0323

05 August 2008

323 Number of Connected Components in an Undirected Graph

题目

You have a graph of 

1

n
nodes. You are given an integer 
1

n
and an array 
1

edges
where 
1

edges[i] = [ai, bi]
indicates that there is an edge between 
1

ai
and 
1

bi
in the graph.

Return the number of connected components in the graph.

Example 1: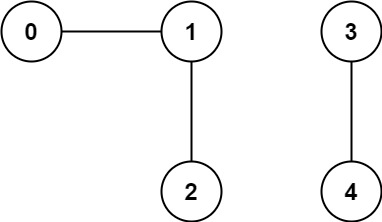

1
2

Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2

Example 2: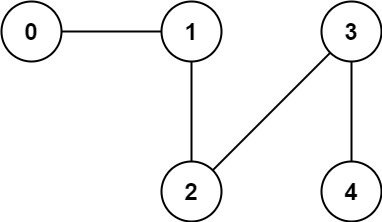

1
2

Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1

Constraints:

  • 1

    1 <= n <= 2000

  • 1

    1 <= edges.length <= 5000

  • 1

    edges[i].length == 2

  • 1

    0 <= ai <= bi < n

  • 1

    ai != bi
  • There are no repeated edges.

分析

求无向图中的连通分量。跟number of Islands以及Friends Cycle一样，同样也是三种解法：DFS，BFS和Union Find。

代码

DFS，对每一块独立的分量进行深搜

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
    public int countComponents(int n, int[][] edges) {
        int count = 0;
        // 邻接表
        List<List<Integer>> adjList = new ArrayList<>();
        boolean[] visited = new boolean[n];

        for (int i = 0; i < n; i++) {
            adjList.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                count++;
                dfs(visited, i, adjList);
            }
        }
        return count;
    }

    private void dfs(boolean[] visited, int index, List<List<Integer>> adjList) {
        visited[index] = true;
        for (int i : adjList.get(index)) {
            if (!visited[i]) {
                dfs(visited, i, adjList);
            }
        }
    }
}

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    public int countComponents(int n, int[][] edges) {
        int count = 0;
        //邻接表
        List<List<Integer>> adjList = new ArrayList<>();
        boolean[] visited = new boolean[n];

        for (int i = 0; i < n; i++) {
            adjList.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }

        for (int i = 0;  i < n; i++) {
            if (!visited[i]) {
                count++;
                Queue<Integer> queue = new LinkedList<>();
                queue.offer(i);
                while (!queue.isEmpty()) {
                    int index = queue.poll();
                    visited[index] = true;
                    for (int next : adjList.get(index)) {
                        if (!visited[next]) queue.offer(next);
                    }
                }
            }
        }
        return count;
    }
}

Union Find

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    public int countComponents(int n, int[][] edges) {
        int[] parents = new int[n];
        Arrays.fill(parents, -1);

        for (int[] edge : edges) {
            int root1 = find(parents, edge[0]);
            int root2 = find(parents, edge[1]);
            if (root1 != root2) {
                parents[root1] = root2;
                n--;
            }
        }
        return n;
    }

    // 这里并查集只实现find即可，无需union
    private int find(int[] parents, int x) {
        int root = x;
        while (parents[root] != -1) {
            root = parents[root];
        }
        return root;
    }
}
This site is open source. Improve this page.