426 Convert Binary Search Tree to Sorted Doubly Linked List
题目
Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.
You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.
We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.
Example 1:
1
2
3
4
5
6
7
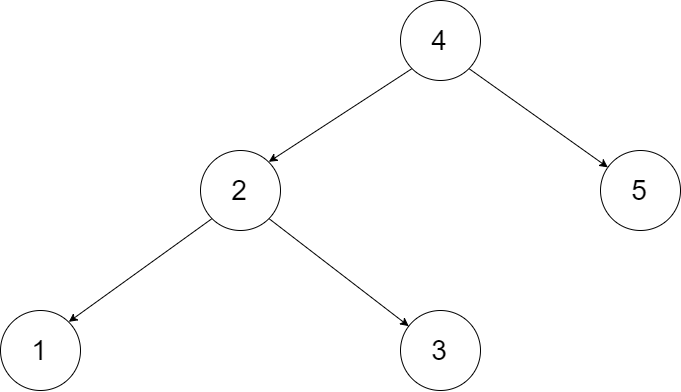
Input: root = [4,2,5,1,3]
Output: [1,2,3,4,5]
Explanation: The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.
Example 2:
1
2
Input: root = [2,1,3]
Output: [1,2,3]
Example 3:
1
2
3
Input: root = []
Output: []
Explanation: Input is an empty tree. Output is also an empty Linked List.
Example 4:
1
2
Input: root = [1]
Output: [1]
Constraints:
- -1000 <= Node.val <= 1000
- Node.left.val < Node.val < Node.right.val
- All values of Node.val are unique.
- 0 <= Number of Nodes <= 2000
分析
这个题要求将一个 二叉搜索树 就地转化为一个已排序好的双向循环链表 。对于双向循环列表,可以将左右孩子指针作为双向循环链表的前驱和后继指针,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。需要返回链表中最小元素的指针。
复习一下树的遍历方式:
总的来说,有两种遍历树的策略:
- 深度优先搜索 (DFS) 在深度优先搜索中,我们以 深度 优先,从根开始先抵达某个叶子,再回退以前往下一个分支。 深度优先搜索又可以根据根节点、左子结点和右子结点的顺序关系分为前序遍历,中序遍历和后序遍历。
- 广度优先搜索 (BFS) 逐层扫描整棵树,按照高度顺序自顶向下。上层的结点比下层更先访问。
下图表示了不同策略下的访问顺序,用 1-2-3-4-5 的顺序来比较不同的策略。

按照题意,利用DFS的中序遍历+备忘录。
标准的中序遍历采用 左 -> 根 -> 右 的顺序,其中 左 和 右 的部分调用递归。 本题的处理在于将前一个结点与当前结点链接,因此,必须跟踪最后一个结点,该结点在新的双向链表中是当前最大的。

同时,也需要保留第一个,也就是最小的结点,以完成闭环。 具体算法:
- 将 first 和 last 结点 初始化为 null。
- 调用标准中序遍历 inOrder(root) :
- 若结点不为 null :
- 调用左子树递归 inOrder(node.left)。
- 若 last 结点不为空,将 last 与当前的 node 链接。
- 否则初始化 first 结点。
- 将当前结点标记为最后 : last = node.
- 调用右子树递归 inOrder(node.right)。
- 将最前与最后的结点链接完成闭环,返回 first
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val,Node _left,Node _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
// 最小的(第一个)和最大的(最后一个)节点
Node first = null;
Node last = null;
public Node treeToDoublyList(Node root) {
if (root == null) {
return null;
}
inOrder(root);
// close DLL
last.right = first;
first.left = last;
return first; // 返回最小值
}
public void inOrder(Node node) {
if (node != null) { //开始中序遍历
// left
inOrder(node.left);
// node
if (last != null) {
// link the previous node (last) with the current one (node)
last.right = node;
node.left = last;
} else {
// keep the smallest node to close DLL later on
first = node;
}
last = node;
// right
inOrder(node.right);
}
}
}