GuilinDev

Lc0986

05 August 2008

986 Interval List Intersections

题目

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval 

1

[a, b]
(with 
1

a <= b
) denotes the set of real numbers 
1

x
with 
1

a <= x <= b
. The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

Example 1:

1
2

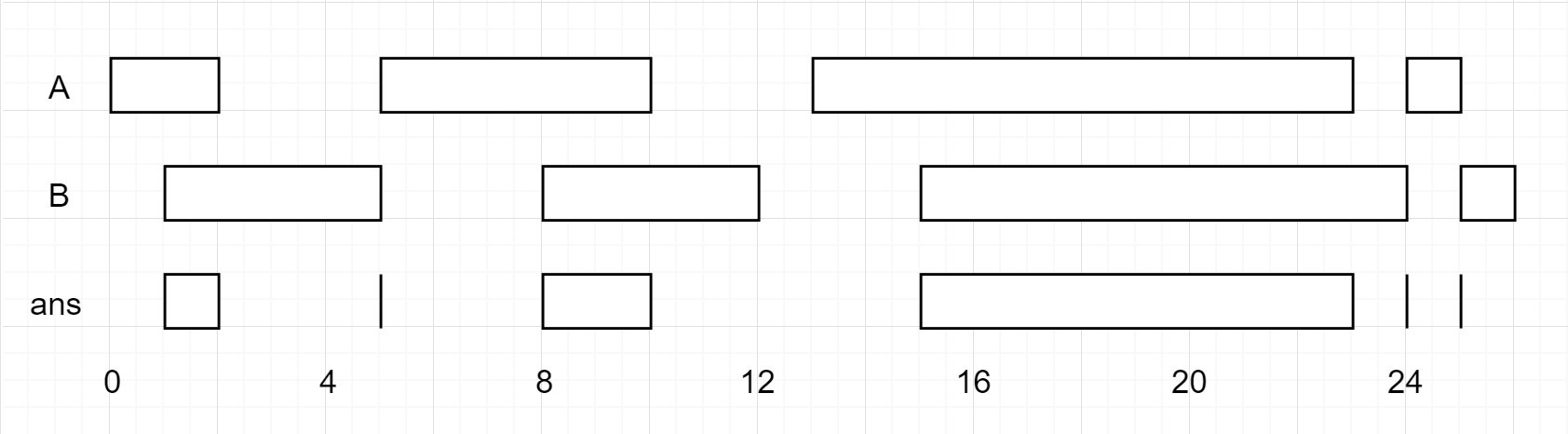
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Note:

  1. 1

    0 <= A.length < 1000

  2. 1

    0 <= B.length < 1000

  3. 1

    0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

分析

我们称 b 为区间 [a, b] 的末端点。在两个数组给定的所有区间中，假设拥有最小末端点的区间是 A[0]，然后，在数组 B 的区间中， A[0] 只可能与数组 B 中的至多一个区间相交。（想象一下，如果 B 中存在两个区间均与 A[0] 相交，那么B中这两个区间都将包含 A[0] 的末端点，但是 B 中的区间应该是不相交的，所以B中最多只有一个区间跟A相交，反之亦然）。

所以如果 A[0] 拥有最小的末端点，那么它只可能与 B[0] 相交。然后我们就可以跳过区间 A[0]，因为它不能与其他任何区间再相交了。相似的，如果 B[0] 拥有最小的末端点，那么它只可能与区间 A[0] 相交，然后我们就可以将 B[0] 删除，因为它无法再与其他区间相交了。

用两个指针来模拟完成跳过A[0] 或 B[0] 的操作。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
    public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
        if (firstList == null || firstList.length == 0 || secondList == null || secondList.length == 0) {
            return new int[0][0];
        }
        List<int[]> results = new ArrayList<>();
        int len1 = firstList.length, len2 = secondList.length;
        int index1 = 0, index2 = 0;
        
        while (index1 < len1 && index2 < len2) {
            int low = Math.max(firstList[index1][0], secondList[index2][0]); // 较大的左边界
            int high = Math.min(firstList[index1][1], secondList[index2][1]); // 较小的右边界
            
            // 这个条件看是否有相交
            if (low <= high) {
                results.add(new int[]{low, high});
            }
            
            // 跳过拥有较小末端点的元素，注意因为上面的条件，这里不会有等于
            if (firstList[index1][1] < secondList[index2][1]) {
                index1++;
            } else {
                index2++;
            }
        }
        
        return results.toArray(new int[results.size() - 1][]);
    }
}
This site is open source. Improve this page.