GuilinDev

Lc1026

05 August 2008

1026 Maximum Difference Between Node and Ancestor

题目

Given the 

1

root
of a binary tree, find the maximum value 
1

V
for which there exists different nodes 
1

A
and 
1

B
where 
1

V = |A.val - B.val|
and 
1

A
is an ancestor of 
1

B
.

(A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.)

Example 1:

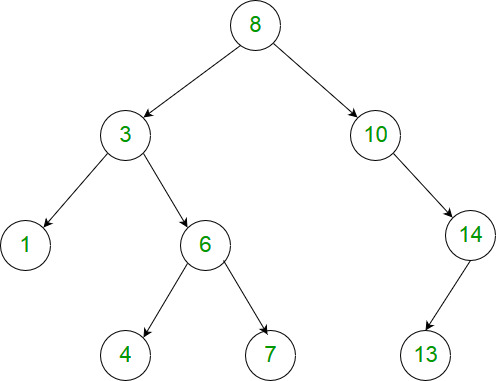
1
2
3
4
5
6
7
8
9

Input: [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: 
We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Note:

  1. The number of nodes in the tree is between 
    1

    2
    and 
    1

    5000
    .
  2. Each node will have value between 
    1

    0
    and 
    1

    100000
    .

分析

寻找当前node的左右子树的最大值和最小值，跟当前node的差值比较，并进行DFS查找。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int result;
    public int maxAncestorDiff(TreeNode root) {
        result = 0;
        if (root == null || (root.left == null && root.right == null)) {
            return 0;
        }
        helper(root, root.val, root.val);
        return result;
        
    }
    private void helper(TreeNode node, int min, int max) {
       
        max = Math.max(max, node.val);
        min = Math.min(min, node.val);
        
        // 打擂台
        result = Math.max(result, Math.abs(max - min));
        
        if (node.left != null) {
            helper(node.left, min, max);
        }
        if (node.right != null) {
            helper(node.right, min, max);
        }
    }
}
This site is open source. Improve this page.