GuilinDev

Lc1206

05 August 2008

1206. Design Skiplist

跳表实现的主要难度在于插入(add)算法。只要把add方法搞明白之后，一切都迎刃而解了。

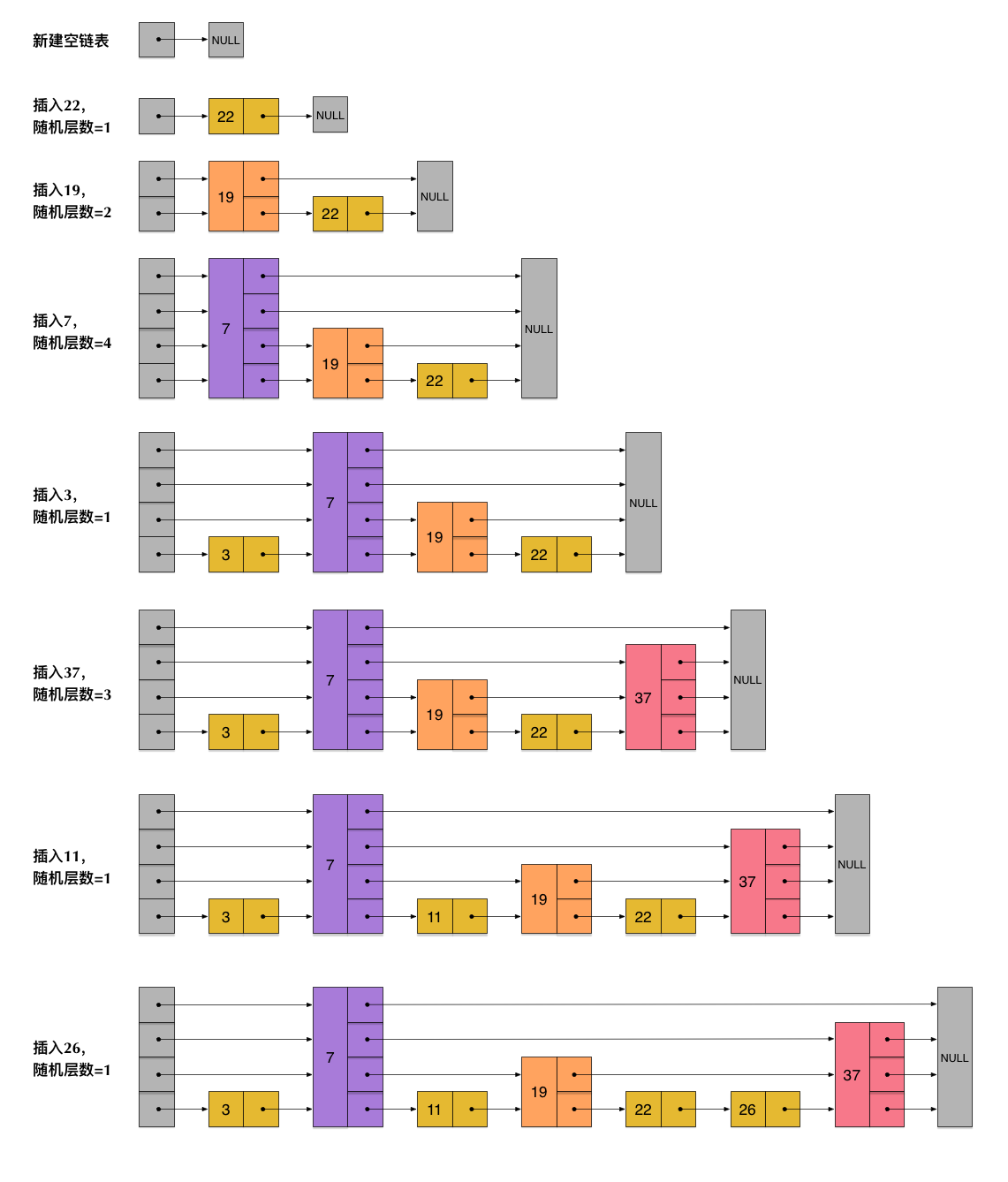
跳表的数据结构

class Node{
    Integer value; //节点值
    Node[] next; // 节点在不同层的下一个节点

    public Node(Integer value,int size) { // 用size表示当前节点在跳表中索引几层
        this.value = value;
        this.next = new Node[size];
    }
}

插入一个节点Node，它到底应该是索引到第几层呢？

如果想着如何准确的维护上一层是下一层的1/2，发现越想越复杂；然后通过相关资料，发现早就给出一个解决方案：随机出来一个层数。

这里有一个疑惑：就凭随机出来的一个层数，能保证查询与插入性能吗？

在分析之前，我们还需要着重指出的是，执行插入操作时计算随机数的过程，是一个很关键的过程，它对skiplist的统计特性有着很重要的影响。这并不是一个普通的服从均匀分布的随机数，它的计算过程如下：

首先，每个节点肯定都有第1层指针（每个节点都在第1层链表里）。

如果一个节点有第i层(i>=1)指针（即节点已经在第1层到第i层链表中），那么它有第(i+1)层指针的概率为p。

节点最大的层数不允许超过一个最大值，记为MaxLevel。

这个计算随机层数的伪码如下所示：

int randomLevel()
    int level = 1;
    while (Math.random()<p && level<MaxLevel){
        level ++ ;
    }
    return level;

randomLevel()的伪码中包含两个参数，一个是p，一个是MaxLevel。在Redis的skiplist实现中，这两个参数的取值为：

p = 1/4

MaxLevel = 32

知道了层数，这下就好办了。思路如下：

先随机出来一个层数，new要插入的节点，先叫做插入节点newNode；
根据跳表实际的总层数从上往下分析，要插入一个节点newNode时，先找到节点在该层的位置：因为是链表，所以需要一个节点node，满足插入插入节点newNode的值刚好不大于node的下一个节点值，当然，如果node的下个节点为空，那么也是满足的。

先把找节点在某一层位置的方法封装起来：

/**
* 找到level层 value 刚好不小于node 的节点
* @param node 从哪个节点开始找
* @param levelIndex 所在层
* @param value 要插入的节点值
* @return
*/
private Node findClosest(Node node,int levelIndex,int value){
    while ((node.next[levelIndex])!=null && value >node.next[levelIndex].value){
        node = node.next[levelIndex];
    }
    return node;
}

确定插入节点newNode在该层的位置后，先判断下newNode的随机层数是否小于当前跳表的总层数，如果是，则用链表的插入方法将newNode插入即可。
如此循环，直到最底层插入newNode完毕。
循环完毕后，还需要判断下newNode随机出来的层数是否比跳表的实际层数还要大，如果是，直接将超过实际层数的跳表的头节点指向newNode即可，该跳表的实际层数也就变为newNode的随机层数了。

理解了插入算法后，查找跟删除就简单多了。

不管是插入、查找还是删除，均是从跳表上层往下层分析，复用上面的findClosest方法，找到要查询的值在该层closest的节点。比如查询，只需要判断findClosest出来的节点值是否等于该查询值即可，是就返回，不是则继续往下层判断。删除方法思想也是一致的。

最终代码

class Skiplist {
    class Node {
        Integer value;
        Node[] next;

        public Node(Integer value, int size) {
            this.value = value;
            this.next = new Node[size];
        }

        @Override
        public String toString() {
            return String.valueOf(value);
        }
    }
    /**
     * 最大层数
     */
    private static int DEFAULT_MAX_LEVEL = 32;
    /**
     * 随机层数概率，也就是随机出的层数，在 第1层以上(不包括第一层)的概率，层数不超过maxLevel，层数的起始号为1
     */
    private static double DEFAULT_P_FACTOR = 0.25;

    Node head = new Node(null, DEFAULT_MAX_LEVEL); //头节点

    int currentLevel = 1; //表示当前nodes的实际层数，它从1开始


    public Skiplist() {
    }

    public boolean search(int target) {
        Node searchNode = head;
        for (int i = currentLevel - 1; i >= 0; i--) {
            searchNode = findClosest(searchNode, i, target);
            if (searchNode.next[i] != null && searchNode.next[i].value == target) {
                return true;
            }
        }
        return false;
    }

    /**
     * @param num
     */
    public void add(int num) {
        int level = randomLevel();
        Node updateNode = head;
        Node newNode = new Node(num, level);
        // 计算出当前num 索引的实际层数，从该层开始添加索引
        for (int i = currentLevel - 1; i >= 0; i--) {
            //找到本层最近离num最近的list
            updateNode = findClosest(updateNode, i, num);
            if (i < level) {
                if (updateNode.next[i] == null) {
                    updateNode.next[i] = newNode;
                } else {
                    Node temp = updateNode.next[i];
                    updateNode.next[i] = newNode;
                    newNode.next[i] = temp;
                }
            }
        }
        if (level > currentLevel) { //如果随机出来的层数比当前的层数还大，那么超过currentLevel的head 直接指向newNode
            for (int i = currentLevel; i < level; i++) {
                head.next[i] = newNode;
            }
            currentLevel = level;
        }

    }

    public boolean erase(int num) {
        boolean flag = false;
        Node searchNode = head;
        for (int i = currentLevel - 1; i >= 0; i--) {
            searchNode = findClosest(searchNode, i, num);
            if (searchNode.next[i] != null && searchNode.next[i].value == num) {
                //找到该层中该节点
                searchNode.next[i] = searchNode.next[i].next[i];
                flag = true;
                continue;
            }
        }
        return flag;
    }

    /**
     * 找到level层 value 大于node 的节点
     *
     * @param node
     * @param levelIndex
     * @param value
     * @return
     */
    private Node findClosest(Node node, int levelIndex, int value) {
        while ((node.next[levelIndex]) != null && value > node.next[levelIndex].value) {
            node = node.next[levelIndex];
        }
        return node;
    }


    /**
     * 随机一个层数
     */
    private static int randomLevel() {
        int level = 1;
        while (Math.random() < DEFAULT_P_FACTOR && level < DEFAULT_MAX_LEVEL) {
            level++;
        }
        return level;
    }
}

/**
 * Your Skiplist object will be instantiated and called as such:
 * Skiplist obj = new Skiplist();
 * boolean param_1 = obj.search(target);
 * obj.add(num);
 * boolean param_3 = obj.erase(num);
 */

This site is open source. Improve this page.