1326 Minimum Number of Taps to Open to Water a Garden
花园浇水需要的最少水龙头
原题
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, …, n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
There is a one-dimensional garden on the x-axis. The garden starts at the point 1
0
1
n
1
n
There are 1
n + 1
1
[0, 1, ..., n]
Given an integer 1
n
1
ranges
1
n + 1
1
ranges[i]
1
i-th
1
[i - ranges[i], i + ranges[i]]
Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.
Example 1: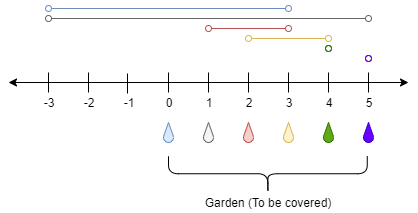
1
2
3
4
5
6
7
8
9
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]
Example 2:
1
2
3
Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.
Example 3:
1
2
Input: n = 7, ranges = [1,2,1,0,2,1,0,1]
Output: 3
Example 4:
1
2
Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4]
Output: 2
Example 5:
1
2
Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4]
Output: 1
Constraints:
1
1 <= n <= 10^4
1
ranges.length == n + 1
1
0 <= ranges[i] <= 100
分析
1)DP,O(N ^ 2)

2)DP小优化,1
O(N * maxRange)

3)贪心
可以将问题转换一下,水龙头浇灌的范围是一个区间,花园的范围也是一个区间。求最小水龙头数,实质上就是求能够覆盖花园整个区间的最小区间数。 那么我们就可以利用贪心来求解问题了。我们的目的是在能够覆盖当前最左范围的所有水龙头中选择灌溉最右范围最大的水龙头。
1.将水龙头按照其能灌溉到的最右位置进行排序;
2.从后往前查找第一个能够灌溉到花园最左边的水龙头,就是我们第一个选择的水龙头(因为我们是按照最右位置的大小排序的)
3.更新左范围为当前所选水龙头最右位置,并删除当前水龙头之前的水龙头即可(并不是真的删除,改一下可用水龙头的index即可) 重复2,3即可。
排序了,O(nlogn)
代码
1)DP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
class Interval {
int start;
int end;
Interval(int start, int end){
this.start = start;
this.end = end;
}
}
public int minTaps(int n, int[] ranges) {
List<Interval> intervals = new ArrayList<>();
int pos = 0;
// 得到所有灌溉区间。
for (int range: ranges){
intervals.add(new Interval(pos - range, pos + range));
pos += 1;
}
int size = intervals.size();
// n + 1个点一共有 n 个区间。 dp矩阵表示前i个区间所需最小的taps
int[] dp = new int[n + 1];
dp[0] = 0;
for (int i = 0; i < n; i++){
dp[i + 1] = Integer.MAX_VALUE;
// 枚举所有覆盖它的区间。
for (int j =0; j < size; j++){
if (intervals.get(j).end < i + 1 || intervals.get(j).start > i){
continue;
}
// 满足:intervals.get(j).start <= i && intervals.get(j).end >= i + 1
int start = intervals.get(j).start >= 0 ? intervals.get(j).start : 0;
if (dp[start] != Integer.MAX_VALUE){
dp[i + 1] = Math.min(dp[i + 1], dp[start] + 1);
}
}
}
return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];
}
}
2)DP优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public int minTaps(int n, int[] ranges) {
int[] dp = new int[n + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
// dp[i] 表示为了覆盖区间 [0,i] 所需要 的最小taps 即前i个数为止的区间。
dp[0] = 0;
// 遍历所有水龙头的位置
for (int i = 0; i <= n; i++){
// 找到当前处的tap能覆盖的最左和最右的位置
int left = Math.max(i- ranges[i], 0);
int right = Math.min(i + ranges[i], n);
for (int j = left + 1; j <= right;j++){
//查看如果用这个tap去覆盖这些位置,所用的水龙头的位置均为前【0,left】区间所需要的水龙头的数量 + 1
if (dp[left] != Integer.MAX_VALUE){
dp[j] = Math.min(dp[j], dp[left] + 1);
}
}
}
return dp[n] == Integer.MAX_VALUE ? -1: dp[n];
}
}
3)贪心
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
//水龙头范围
class Range{
public Range(int l, int r) {
this.l = l;
this.r = r;
}
int l;
int r;
}
//计数君
class IntHolder{
int cnt = 0;
}
public int minTaps(int n, int[] ranges) {
Range[] Ranges = new Range[ranges.length];
for(int i = 0; i < ranges.length; i++) {
Range ran = new Range(i-ranges[i], i+ranges[i]);
Ranges[i] = ran;
}
//将水龙头按最右位置排序
Arrays.sort(Ranges, new Comparator<Range>() {
@Override
public int compare(Range r1, Range r2) {
return r1.r-r2.r;
}
});
IntHolder intholder = new IntHolder();
boolean flag = match(0, n, 0, Ranges, intholder);
if(flag) return intholder.cnt;
return -1;
}
/**
* 是否能够灌溉到当前左边界到右边界
*
* @param lrange 左边界
* @param rlange 右边界
* @param lindex 可选水龙头的起始索引
* @param Ranges 水龙头范围数组
* @param intholder 计数君
* @return 是否能够灌溉到当前lrange-rlange
*/
public boolean match(int lrange, int rlange, int lindex, Range[] Ranges, IntHolder intholder) {
boolean isMatch = false;
for(int i = Ranges.length-1; i >= lindex; i--) {
//灌溉了整个区间
if(Ranges[i].l <= lrange && Ranges[i].r >= rlange) {
intholder.cnt++;
return true;
}
//能灌溉到左边界
if(Ranges[i].l <= lrange) {
intholder.cnt++;
isMatch = match(Ranges[i].r, rlange, i+1, Ranges, intholder);
break;
}
}
//若不能灌溉到当前左边界,则返回false,能灌溉到则返回true
return isMatch;
}
}