GuilinDev
Lc1539
05 August 2008
1539. Kth Missing Positive Number
给一个 严格升序排列 的正整数数组 arr 和一个整数 k 。
找到这个数组里第 k 个缺失的正整数。
示例 1：
1
2
3
输入：arr = [2,3,4,7,11], k = 5
输出：9
解释：缺失的正整数包括 [1,5,6,8,9,10,12,13,...] 。第 5 个缺失的正整数为 9 。
示例 2：
1
2
3
输入：arr = [1,2,3,4], k = 2
输出：6
解释：缺失的正整数包括 [5,6,7,...] 。第 2 个缺失的正整数为 6 。
思路1 - 枚举
首先明白题意，缺失的数一定是从 1 开始判断，而且题目中的数组已经严格升序了，那就好办了。
使用 cur 表示当前位置应该出现的数，如果数组中该位置上的数和 cur 不相等，说明 cur 缺失了，就将 k - 1，并且把 cur + 1，因为刚刚那个缺失的 cur 已经计算过了。接着，我们再来看数组中这个位置上的数是不是 cur + 1，如果还不是，那继续 k - 1，cur + 1；如果是，说明 cur + 1 出现了即没有缺失，那我们就判断数组的下一位是不是 cur + 2 ……
最后可能会有一种情况，那就是数组已经遍历完了但是 k 还没有减到 0，这就说明缺失的第 k 个数是超过数组的最后一个数的，这里我们需要做个特殊处理，其实就是 (数组的最后一个数 - 1) + 剩余的 k 值 就行了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public int findKthPositive(int[] arr, int k) {
// 当前位置应当出现的数
int cur = 1;
int i = 0;
while (i < arr.length) {
if (cur != arr[i]) {
// cur 缺失
k--;
if (k == 0) {
return cur;
}
cur++;
} else {
i++;
cur++;
}
}
// 遍历完数组但是 k 还没有减完
return (cur - 1) + k;
}
}
思路2 - 二分搜索
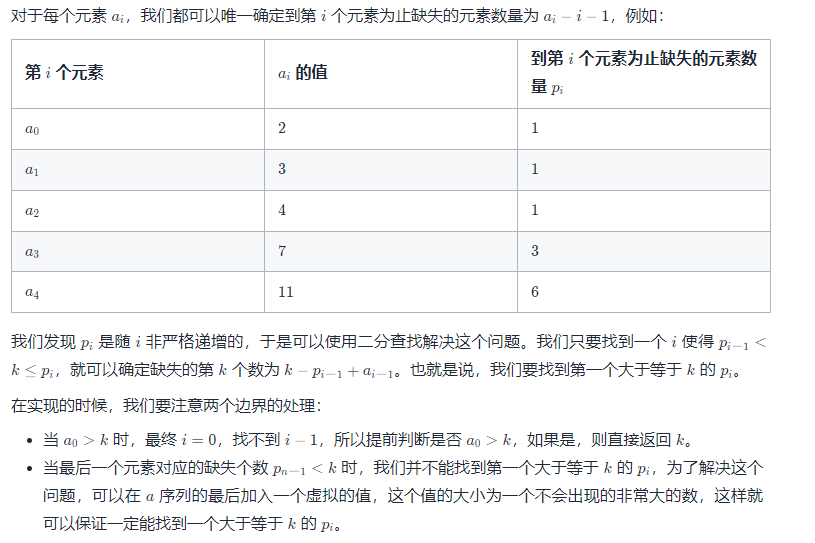
时间复杂度：O(logn)，其中 n 是数组 arr 的长度。即二分查找的时间复杂度。
空间复杂度：O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public int findKthPositive(int[] arr, int k) {
if (arr[0] > k) {
return k;
}
int left = 0, right = arr.length;
while (left < right) {
int mid = (left + right) >> 1;
int x = mid < arr.length ? arr[mid] : Integer.MAX_VALUE;
if (x - mid - 1 >= k) {
right = mid;
} else {
left = mid + 1;
}
}
return k - (arr[left - 1] - (left - 1) - 1) + arr[left - 1];
}
}