GuilinDev

Lc1644

05 August 2008

1644 Lowest Common Ancestor of a Binary Tree II $

Given the ‘root’ of a binary tree, return the lowest common ancestor (LCA) of two given nodes, ‘p’ and ‘q’. If either node ‘p’ or ‘q’ does not exist in the tree, return ‘null’. All values of the nodes in the tree are unique.

According to the definition of LCA on Wikipedia: “The lowest common ancestor of two nodes ‘p’ and ‘q’ in a binary tree ‘T’ is the lowest node that has both ‘p’ and ‘q’ as descendants (where we allow a node to be a descendant of itself)”. A descendant of a node ‘x’ is a node ‘y’ that is on the path from node ‘x’ to some leaf node.

Example 1:

1
2
3

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

1
2
3

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5. A node can be a descendant of itself according to the definition of LCA.

Example 3:

1
2
3

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 10
Output: null
Explanation: Node 10 does not exist in the tree, so return null.

Constraints:

  • The number of nodes in the tree is in the range ‘[1, 104]’.
  • ‘-109 <= Node.val <= 109’
  • All ‘Node.val’ are unique.
  • ‘p != q’

Follow up: Can you find the LCA traversing the tree, without checking nodes existence?

分析

跟236比较，结点自己可以作为自己的后裔。

This question is similar to 236. Last Common Ancestor of Binary Tree. Question 236 has two important premises:

  1. It is guaranteed that both p and q are in the tree.
  2. A node can be a descendant of itself.

In the case of p = 5 and q = 4:
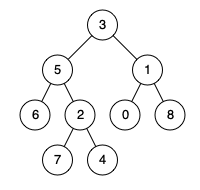
image

Because of the premises, we can return either p OR q as soon as we find one of them. Here is the code:

’'’text public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root == p || root == q || root == null) return root; TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q); return left == null ? right : right == null ? left : root; } ‘’’

But for this question, the premises are different:

  1. It is NOT guaranteed that both p and q are in the tree.
  2. A node can still be a descendant of itself.

Hence,

  1. We need a way to record if we’ve seen both p and q
  2. We need to traverse the entire tree even after we’ve found one of them.

Here are the differences in code. The rest is the same.

  1. Use either ‘boolean’ or integers as flags
  2. Keep traversing down the entire tree. If you return early, the above example would be null, because the code stops when it finds 5 and does not keep searching for 4.

代码

Solution 1: Use 2 booleans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    boolean pFound = false;
    boolean qFound = false;

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        TreeNode LCA = LCA(root, p, q);
        return pFound && qFound ? LCA : null;
    }
    
    public TreeNode LCA(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) return root;
        TreeNode left = LCA(root.left, p, q);     
        TreeNode right = LCA(root.right, p, q);
        if (root == p) {
            pFound = true;
            return root;
        }
        if (root == q) {
            qFound = true;
            return root;
        }
        return left == null ? right : right == null ? left : root;
    }
}

Solution 2: Use integers

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class Solution {
	int count = 0;
	
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        TreeNode LCA = LCA(root, p, q);
        return count == 2 ? LCA : null;
    }
    
    public TreeNode LCA(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) return root;
        TreeNode left = LCA(root.left, p, q);     
        TreeNode right = LCA(root.right, p, q);
        if (root == p || root == q) {
            count++;
            return root;
        }
        return left == null ? right : right == null ? left : root;
    }
}

Time Complexity: O(N)
Space Complexity: O(H), H is the height of the tree

This site is open source. Improve this page.