GuilinDev
Pagerank Algorithm
09 September 2020
PageRank是一种对网页进行排名的直观方法，它是Google早期阶段的网络索引算法的基础。这里我们从以下几个方面来了解PageRank：
- PageRank背后的基本思想
- 了解PageRank算法
- 实现一个PageRank
PageRank背后的基本思想
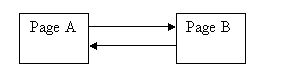
PageRank是基于这样的想法，即网页的受欢迎程度不仅取决于传入链接的数量，还取决于传入链接的类型。排名较高的网页的引用比排名较低的网页贡献更多。图中Fig.1所示的网页B引用的网页A的页面等级为等式：
- PR(A): 页面A的PageRank
- PR(B): 页面B的PageRank
- P(B, A): 从页面B链接去页面A的可能性，这里设为1
- d: 阻尼因数，以增加方程的随机性。
然后计算整个网页图上的PageRank，直到收敛到最终值为止。
了解Page Rank算法
PageRank如何工作如图2所示。需要注意的是，如果存在没有出站链接的网页，则不会对页面排名有所贡献（通常被称为悬挂页面）。
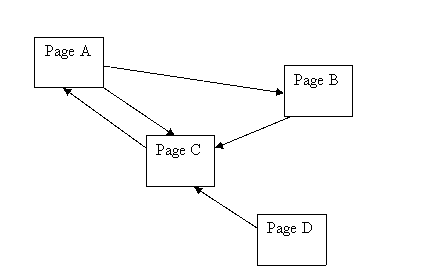
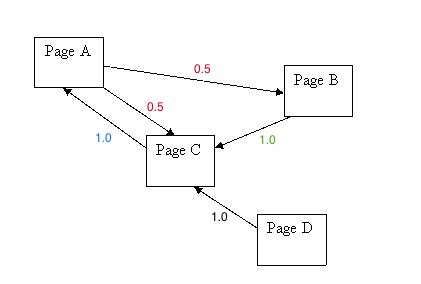
最初，所有网页的页面排名取为1。边缘的权重，也就是是从网页X到Y的概率（网页A具有2个链接，因此，访问每个网页的概率是1/2）。用概率表示网络图之后，网络图看起来类似于Fig3。每个网页的页面等级通过应用PageRank公式确定，重复该过程，直到算法收敛得到结果为止，也即页面等级的值变化不超过小值（通常称为epsilon，通常固定为1e-4）。引入的阻尼因子（d）是在Web图上添加一些随机性，即d是用户将移动到链接的网页的概率，而1-d是选择随机网页的概率，通常取为0.85。
对于迭代：
PR(C)=(1-d) + d( P(A,C)PR(A) + P(B,C)PR(B) + P(D,C)PR(D)) PR(C)=(0.15)+ 0.85( 0.51 + 11 + 11) = 2.275
PR(C) 可以由矩阵乘积得到：
类似地，将方程式扩展到所有网页，得出方程式
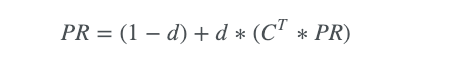
其中，矩阵C表示概率转换（C [i] [j] = 用户从页面i转换到页面j的概率）。示例的C矩阵可以表示为上面表示的矩阵。同样，初始页面等级被分配为所有网页1。计算网页的PR，直到PR收敛到某个值为止。
实现一个PageRank
用Python实现一个简单的PageRank
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
def pagerank(C, eps=0.0001, d=0.85):
P = np.ones(len(C))
while True:
P_ = np.ones(len(A)) * (1 - d) + d * C.T.dot(P)
delta = abs(P_ - P).sum()
if delta <= eps:
return P_
P = P_
p = pagerank(C)
# Result
# p=[1.16, 0.644, 1.19, 0.15]
最后结果C > A > B > D，注意有些网页incoming links少，但是排名依然比较高，例如A。